Coordinate Geometry is a simple method of analyzing geometrical shapes. It is one of the most scoring topics of IIT JEE Math course. After calculus, it is the only syllabus that can get you full marks. The topic covers:
- Straight Lines
- Hyperbola
- Ellipse
- Parabola
- Circle
Here are few short cuts that you should never forget:
- If ABCD is a parallelogram, then D= A-B+C
· Area of Rhombus framed by ax (+ or -) by (+or -) c = 0 is calculated by 2c2/ab
· The equation of line parallel to X axis is form = k
· If a line slope passes through (x1, y1) and (x2, y2) is (y2-y1)(x2-x1) only when x1is not equal to x2
· The equation of a line running parallel to x- axis is of the form y=k
· The equation of a line with m slope and intercept y is y= mx+c
· The equation of line for non- zero intercept and b on x and y axis is (x/a) + (y/b)= 1
· The intersection point of two lines, that don’t run parallel can be detected by solving them simultaneously
· ax+ by + c= 0
· y= mx +b where m= slope and b =y – intercept
· y- y1 = m (x- x1), where m= slope and the lines passes via (x1, y1)
· Three points X Y and Z are collinear if (slope (xy) = Slope (yz). This is the right collinearity test
- Tangents are drawn to the circle x^2 + y^2=12 at the points where it is met by the circle x^2 +y^2 – 5x + 3y – 2=0.Find the point of intersection of these tangents
- Solve both the equations for x as well as y
- Method:
- x^2 + y^2=12
- When you put this in the second equation, you get -5x +3y =-10, thus, x= (3y +10)/5
- So [(3y+10)/5]2 + y2 = 12. Now get y and find x and eventually you will get first circle tangent and then intersection points of the tangents
Slope of a Line
The tangent of angle made by a line with positive in clockwise direction is said to be the slope of the line which is marked by letter m.
If (x1, y1) and (x2, y2) are two points on a line, you can find the slope as slope(m)= (y2-y1)/ (x2-x1)
- Conditions for Two Lines to be Parallel or Perpendicular
- Two lines with slopes supposedly, m1 and m2:
they would be parallel if m1=m2
they will be perpendicular if m1 . m2 = -1
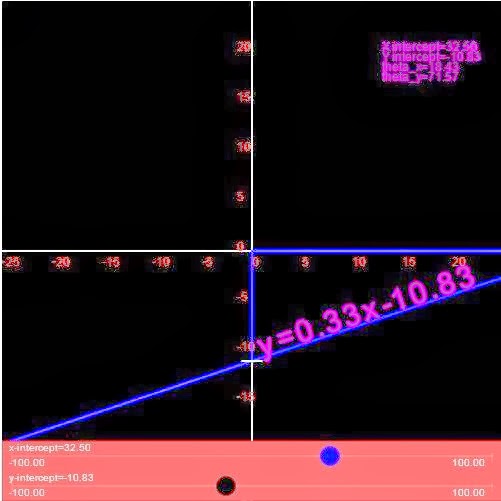
- How to identify Slope, X-Intercept, Y-Intercept from an equation of a line
- The given equation is ax+by+c=0
->m=-a/b
->x-intercept=-c/a
->y-intercept=-c/b
- A line crosses via (2,2) and stands perpendicular to 3x+y = 3. What is the –intercept of the line
- Slope of the line = -1 /slope of 3x+y= 3
- Thus the Slope is 1/3
- The equation formed is y – 2/ x- 2 = 1/3
- In other words, x- 3y +4 = 0
- Thus, Y intercept is 4/3